
A sliver is a small artifact often resulting from a Boolean operation between polygons. Or it may be a small artifact in the input layout data that you wish to remove. Very often it is generated when subtracting a shape that was originally an arc. Slivers end up isolated from the main body.
In order to find and remove slivers, we first must define a parameter that somehow defines it, and which is derived from the characteristics of the polygon. We want the computation to be fast and efficient since we may need to evaluate thousands of polygons. We define a polygon's sliver parameter as:
2 x Area
sliver parameter = ------------
perimeter
Let's start with simple shapes - a circle and a square.
for a square of side = s, the sliver parmeter (SP) is:
2 * s2 s
SP = ----------- = ---
4s 2
So it's clear that as the side of the square goes down, the sliver parameter also goes down. This means that by selecting the appropriate sliver parameter we could separate out all squares with edges smaller than the specified amount.
for a circle of radius r, the sliver parameter is:
2 * πr2
SP = --------- = r
2πr
So like the square, the sliver value for a circle is linearly related to the radius.
Triangles?
Slivers are almost never square or round. They generally look like long narrow triangles. So what is a triangle's sliver parameter?The chart below compares a square, rectangle and triangle

We can see that long/narrow polygons have a low sliver parameter. We can use this information to remove them from the output.
In the snapshot below you can see a circuit board pad surrounded by groundplane with several tiny slivers in the group plane that were generated when the stroked fills did not exactly overlap.
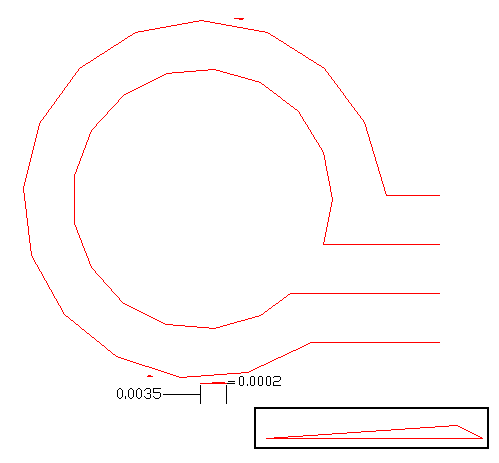
In this example we can approximate the sliver by a triangle with base 0.0002 inch and height 0.0035 inch. This gives a silver parameter (in inches) of
2 x 1/2 0.0002 x 0.0035 ------------------------ = ,000097 0.0035 + 0.0035 + 0.0002
If the user enters a sliver parameter of 0.0001 or larger then this sliver will be removed.